2024年末までの輸入確定値が出たので、2005年~2024年まで、過去20年間のアメリカの日本からの輸入額について、時系列でモデルを設定し、2025年を予測してみた。今回も”やってみる”という意図なので、非常に単純に輸入額のみで試してみる。
元データは、↓ からダウンロード可能です。
まず、輸入額の傾向をみてみる。
# ライブラリーの読み込み
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
# データの読み込み
df = pd.read_csv("japan_import.csv")
df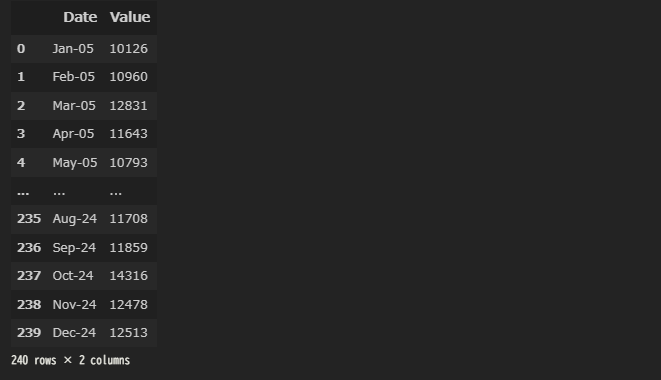
# 可視化
df = df.set_index('Date')
df.plot(figsize=(15,5))
# 平均
print('平均=',df['Value'].mean(), '百万ドル')
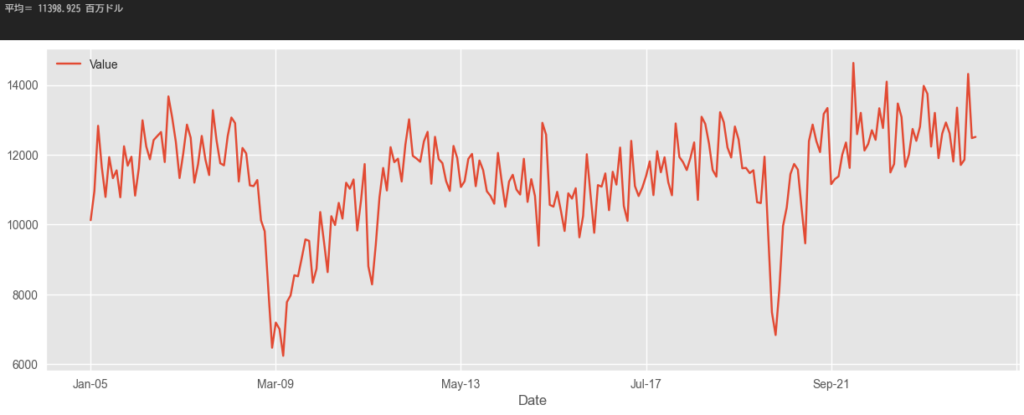
平均は11,399百万ドル
# ライブラリーの追加
from scipy import signal
from statsmodels.tsa.seasonal import STL
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# STL分解
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = [12, 10]
stl = STL(df['Value'],period=12, robust=True).fit()
stl.plot()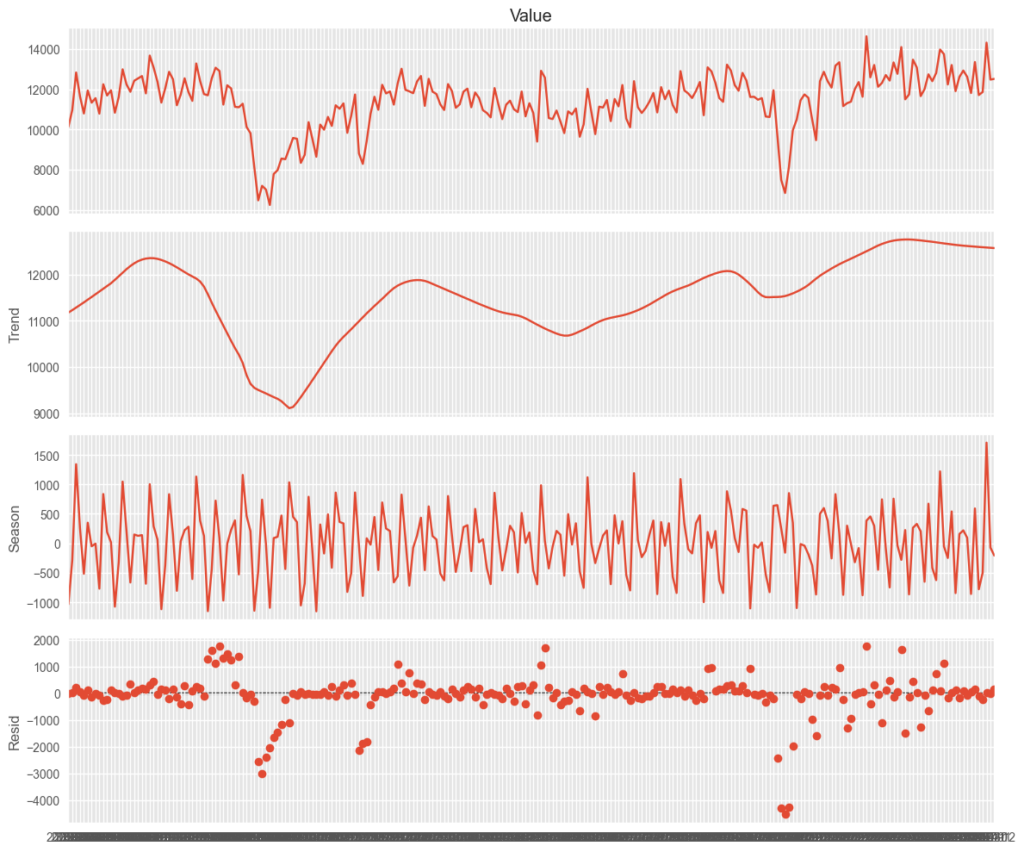
異常値的に、リーマンショックの2009年前後、2002年のコロナ禍で、大きく落ち込むが、リーマンショックの方が、影響も大きく長かったことが見て取れる。今回は、ダミー設定せずに、そのまま使ってみる。
定常性の確認
# ADF検定
dftest = adfuller(df['Value'])
print(dftest[0])
print(dftest[1])
for i, j in dftest[4].items():
print('\t', i, j)
P値は、0.05より大きく、定常性がないので、一回差分をとってみる。
# 差分1をとる
df_d1 = df.diff(1).dropna()
df_d1.plot(figsize=(15,5))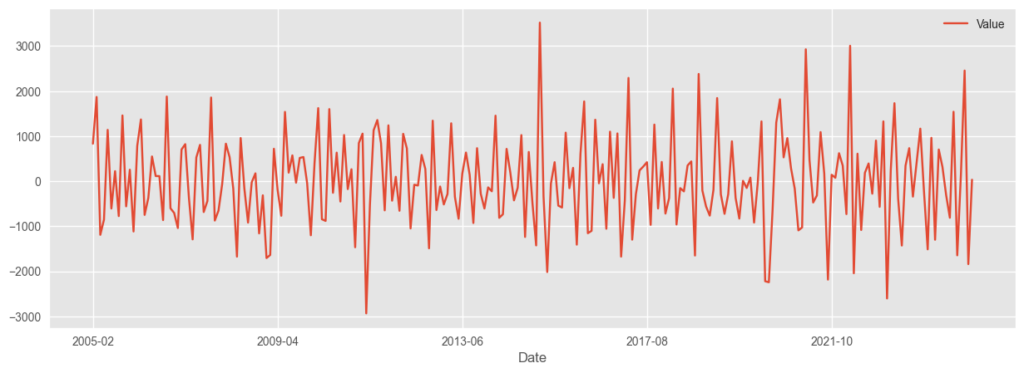
再度、ADF検定
# 再度、ADF検定
dftest = adfuller(df_d1)
print(dftest[1])
for i, j in dftest[4].items():
print('\t', i, j)
P値は0.05より小さく、定常性が確認できた。自己相関、偏自己相関をみてみる。
# 再度、自己相関、偏自己相関を確認
acf = plot_acf(df_d1['Value'], lags=36)
pacf = plot_pacf(df_d1['Value'], lags=36)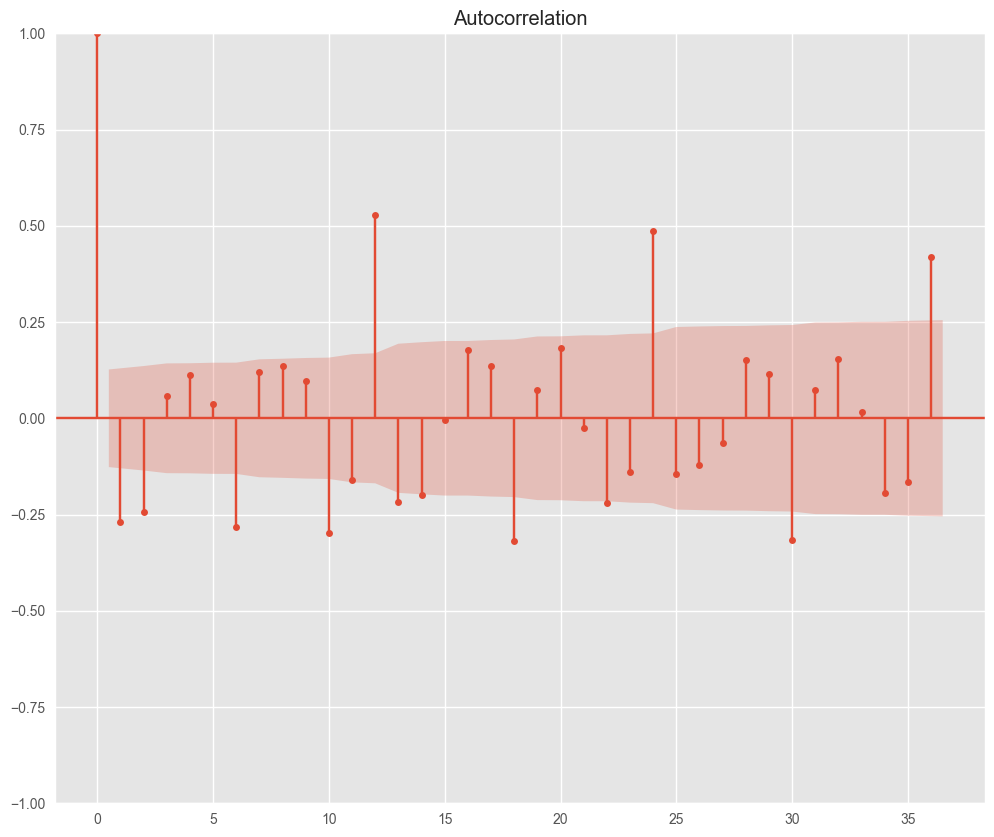
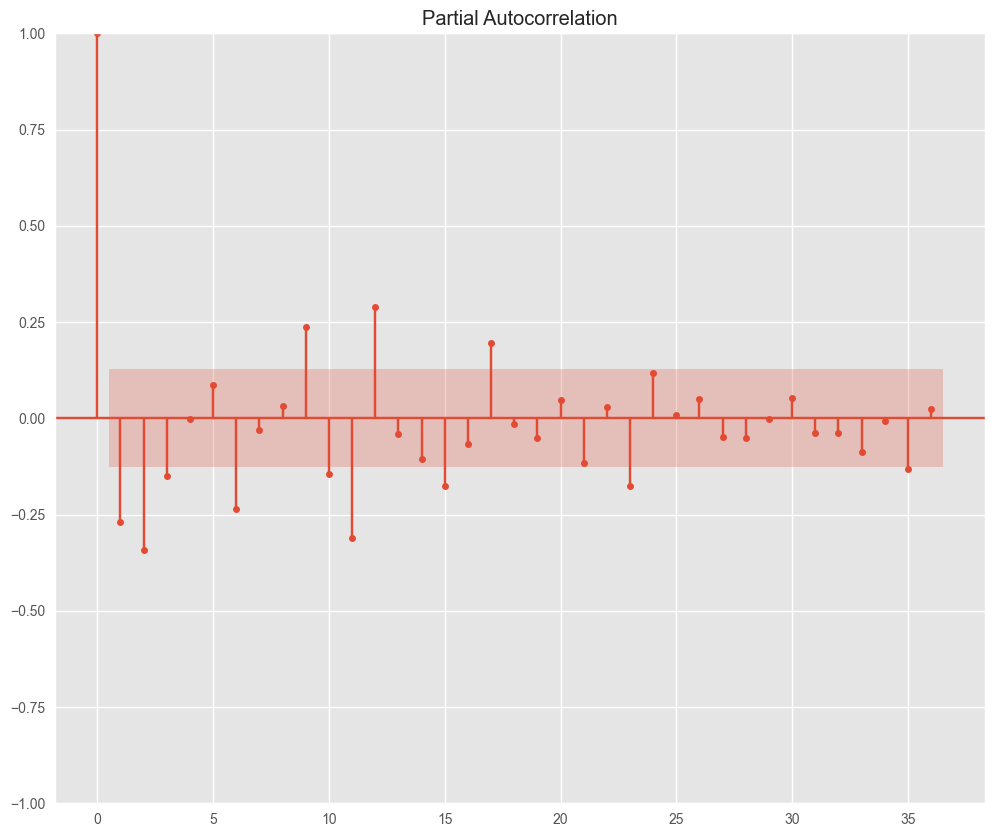
12ケ月毎の周期性がみてとれる。モデルを設定してみる。
# 時系列モデル
#ライブラリーの追加
import pandas as pd
from pmdarima import auto_arima
from pmdarima.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, mean_absolute_error, mean_absolute_percentage_error
# テスト期間は、2024年1年間とする。
train, test = train_test_split(df, test_size=12)# データをモデルに当てはめていく。ARIMA系モデルには手動でモデルや引数内の次数を設定するものと、自動で設定してくれるものを選ぶことができる。
# 自動で設定してみる。自動設定はpmdarimaのauto_arimaで可能。
arima_model = auto_arima(train, seasonal=True, m=12)# モデルと残差の確認
arima_model_fit = arima_model.fit(train)
print(arima_model_fit.summary())
arima_model_fit.plot_diagnostics(figsize=(10,8))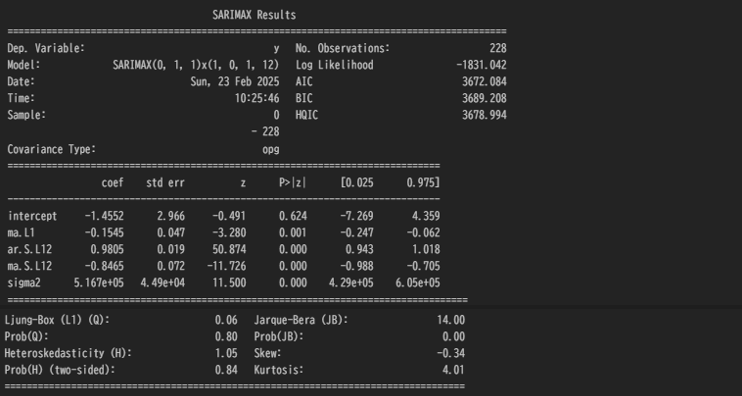
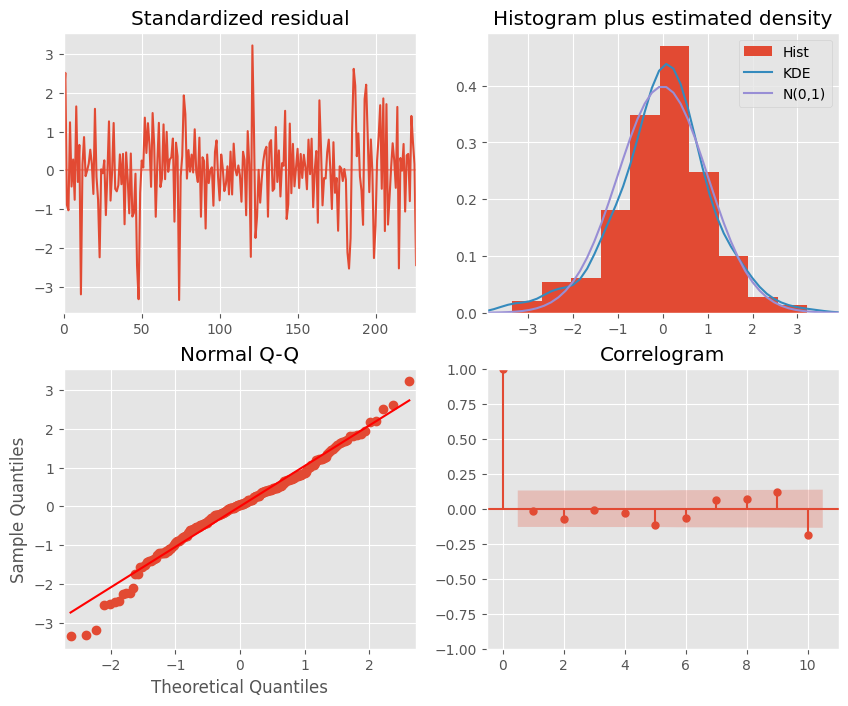
モデルとしては、AR(1)、MA(1)を選択しており、残差も問題なさそう。
# モデル予測
train_pred = arima_model.predict_in_sample()
test_pred = arima_model.predict(n_periods=12)
# 予測値の評価
import numpy as np
MSE = np.sqrt(mean_squared_error(test['Value'], test_pred))
MAE = mean_absolute_error(test['Value'], test_pred)
MAPE = mean_absolute_percentage_error(test['Value'], test_pred) * 100
print(f"MSE: {round(MSE, 3)}")
print(f"MAE: {round(MAE, 3)}")
print(f"MAPE: {round(MAPE, 3)}", '%')
平均が11,399百万ドル(約1.7兆円)で、モデルの制度は4.9%で、誤差の範囲は641百万ドル(約962億円)。
# テスト期間(2024年)+2025年12月までを含めた予測
test_pred2025 = arima_model.predict(n_periods=24)
test_pred2025 
# データの整理
test_pred2 = pd.DataFrame(test_pred2025)
test_pred2 = test_pred2.rename(columns={0:'Value'})
train_pred2 = pd.DataFrame(train_pred)
train_pred2 = train_pred2.rename(columns={'predicted_mean':'Value'})
# 予測値のマージ
df_eva = pd.concat([train_pred2, test_pred2], axis=0)
df_eva = df_eva.rename(columns={'Value':"Pred"})
df_eva
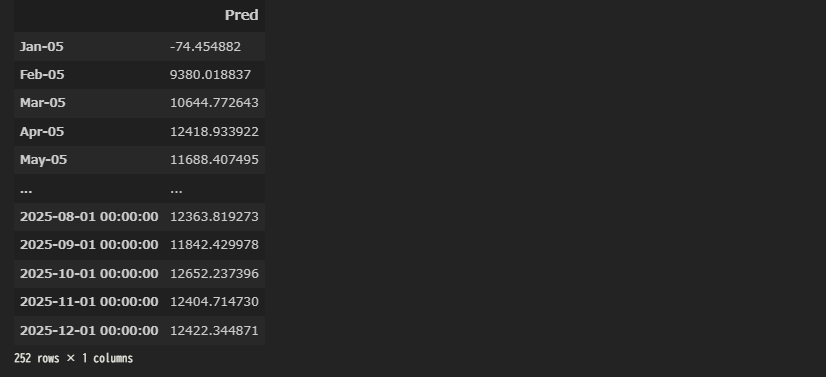
# 実輸入額と予測値を1つのファイルにまとめる
df2025 = df.reset_index(drop=True)
df_eva = df_eva.reset_index(drop=True)
df_eva2025 = df_eva.copy()
df_eva2025['Value'] = ''
df_eva2025['Value'] = df2025['Value']
df_eva2025
# 2005年1月の予測値がマイナスでおかしいので、カット
df_eva2025 = df_eva2025[1:]
# 2005年2月~を改めてindexとして設定
df_eva2025['Date'] = pd.date_range(start='2005-2-1', end='2026-1-1', freq='M')
df_eva2025['Date'] = pd.to_datetime(df_eva2025['Date'])
df_eva2025.set_index('Date', inplace=True)
df_eva2025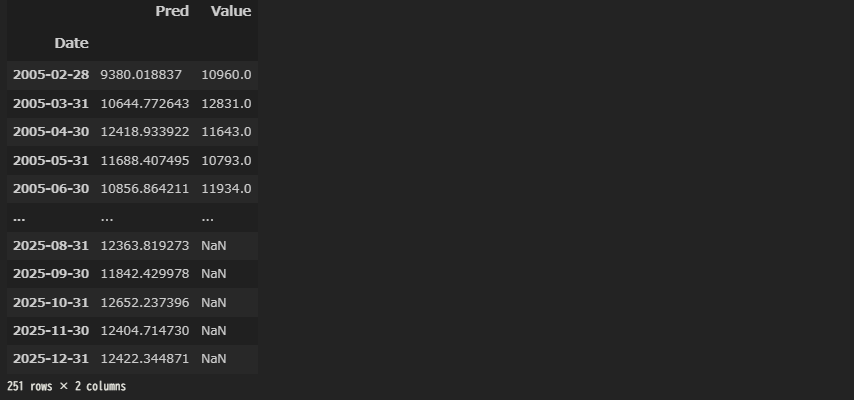
# 描画
fig, ax = plt.subplots(figsize=(20,7))
ax.plot(
df_eva2025.index,
df_eva2025['Value'],
label="Actual")
ax.plot(
df_eva2025.index,
df_eva2025['Pred'],
label="Prediction")
fig.legend()
fig.show()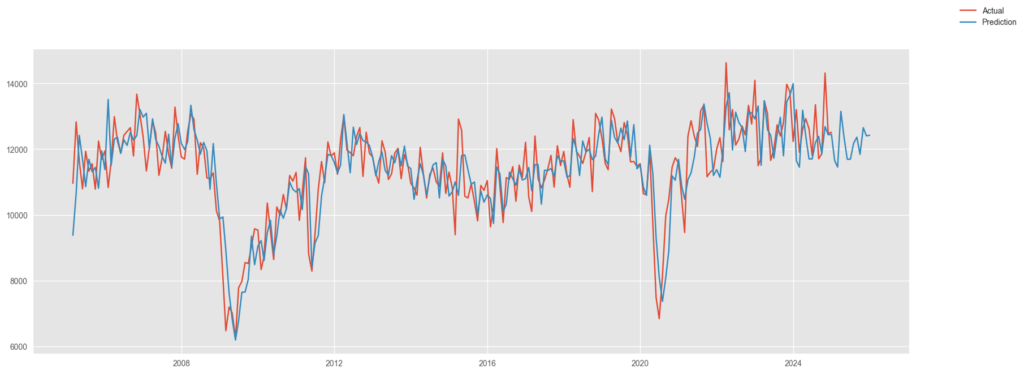
リーマンショックもコロナ禍も傾向としては、うまく対応できていると思える。
2024年~2025年(予測)部分のみ描画してみる。
fig, ax = plt.subplots(figsize=(20,7))
ax.plot(
df_eva2025.index[-24:],
df_eva2025['Value'][-24:],
label="Actual")
ax.plot(
df_eva2025.index[-24:],
df_eva2025['Pred'][-24:],
label="Prediction")
fig.legend()
fig.show()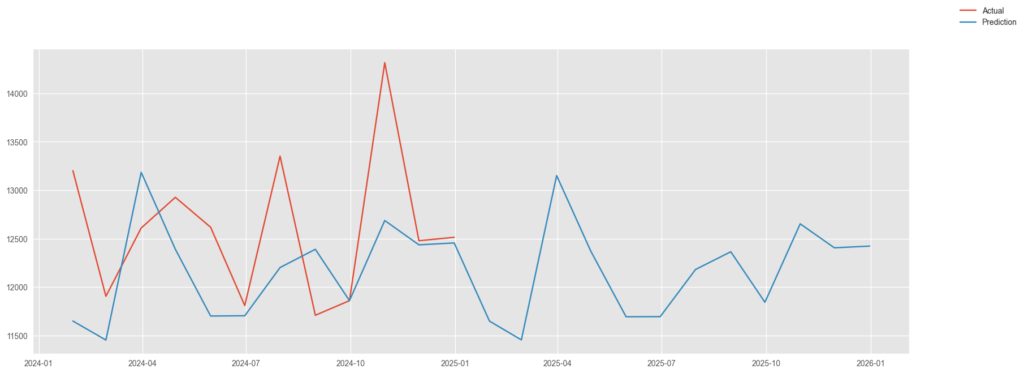
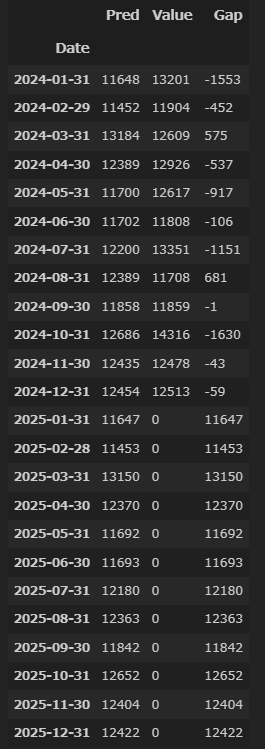
予測値及び2024年の残差は以下のとおり(Pred:予測額、Value:実輸入額、Gap:予測値ー実輸入額)(単位:百万ドル)。2025年は、2024年より少し落ちた額との予測になっている。2025年は、関税なども含め大きく変動していくと思われる。もちろん、輸入額のみでの予測なので、精度も非常にいいとは言えないが、ひとつの参考基準として、この予測額と比べたいと思う。